import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import tensorflow as tf
import keras
import numpy as np
import matplotlib.pyplot as pltFlow matching
In this notebook, we will create our own flow matching network, and train it to reproduce the “datasaurus” distribution.
We will use the simplest form of a flow matching.
The data
The data set stored in the datasaurus.csv file can be downloaded from the website of the seminar. Download the file in wherever you run this notebook.
We read the notebook into a numpy array and also rescale the data.
data = np.genfromtxt("datasaurus.csv", delimiter=",", skip_header=1)
data = data/10 - 5
f=plt.scatter(data[:,0], data[:,1], s=5, alpha=0.5)
f=plt.xlim(-5, 5)
f=plt.xlim(-5, 5)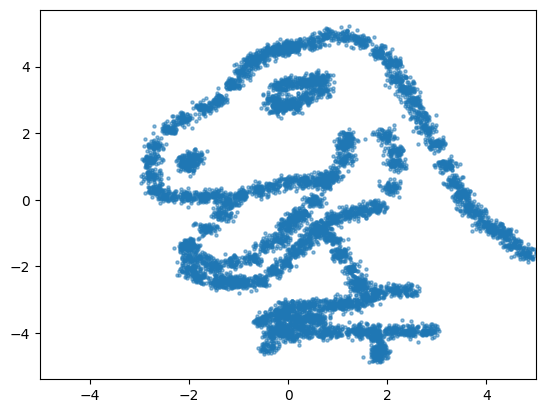
The model
The flow matching model is composed of a single MLP network that will take in the samples \(x_t \in \mathbb{R}^2\) concatenated with the time variable \(t \in [0, 1]\), and outputs a velocity vector \(v_\theta(x_t, t) \in \mathbb{R}^2\).
The samples x_t are computed by linearly interpolating between samples \(x_0\) (sampled from the base distribution) and \(x_1\) (sampled from the data distribution):
\[ x_t = (1-t) x_0 + t x_1. \]
For sampling, we will implement a basic ODE solver. We will approximate the trajectory of a sample from point \(x_0\) into point \(x_1\) by moving the point along its velocity in a series of small time steps of \(dt\). At each time step, we will approximate the “midpoint” velocity, that is, a velocity that we would expect in the middle of the step (at \(t + dt/2\)). In each step, we go from point \(x_t\) to point \(x_{t+dt}\) as follows,
\[ \begin{aligned} v_t & = v_\theta(x_t, t) \\ \hat{x}_\text{midpoint} & = x_t + v_t \times dt/2 \\ \hat{v}_\text{midpoint} & = v_\theta(\hat{x}_\text{midpoint}, t+dt/2) \\ x_{t+dt} & = x_t + \hat{v}_\text{midpoint} \times dt. \end{aligned} \]
We will make these steps all the way from \(x_0\) to \(x_1\), where the intial points are sampled from the base distribution \(x_0 \sim \text{Normal}(0, I)\).
class FlowMatching(keras.Model):
def __init__(self, n_units, n_layers, dim=2):
""" Initiate the flow matching model object
Parameters
----------
n_units: int
Number of units per each layer of the velocity MLP
n_layers: int
Number of layers of the velocity MLP
dim: int
Number of output dimensions (by default 2 because the datasaurus lives in 2D)
"""
super(FlowMatching, self).__init__()
self.dim = dim
self.velocity = keras.Sequential(
[keras.layers.Dense(n_units, activation="elu") for _ in range(n_layers)]
)
self.velocity.add(keras.layers.Dense(dim))
def call(self, inputs):
""" Call the velocity vector
Parameters
----------
inputs: dict
x_0: samples from the base distribution
x_1: samples from the data distribution
t: samples of the time variable between [0, 1]
Returns the velocity vector
"""
x_0, x_1, t = inputs.values()
x_t = (1-t)*x_0 + t*x_1
x = keras.ops.concatenate([x_t, t], axis=-1)
return self.velocity(x)
def step(self, x, t, dt):
""" Make one step using the midpoint ODE solver
Parameters
----------
x: tensor/array (batch_size, dim)
Samples of the variable x_t
t: tuple/array (batch_size,)
Samples of the time variable between [0, 1]
dt: float
The size of the time step
Returns: tensor/array (batch_size, dim)
Samples of the variable x_{t+dt}
"""
t_start = np.zeros_like(x) + t
input_start = keras.ops.concatenate([x, t_start], axis=-1)
v = self.velocity(input_start)
x_mid = x + v * dt / 2
t_mid = t_start + dt / 2
input_mid = keras.ops.concatenate([x_mid, t_mid], axis=-1)
v = self.velocity(input_mid)
x_end = x + v * dt
return x_end
def run(self, x, steps):
""" Run the ODE solver from t=0 to t=1
Parameters
----------
x: tensor/array (batch_size, dim)
Samples from the base distribution, x_0
steps: int
Number of steps to make between t=0 and t=1
Returns: tensor/array (batch_size, dim)
Samples x_1 ~ p_1
"""
time = np.linspace(0, 1, steps+1)
output = []
output.append(x)
for i in range(steps):
x = self.step(x, time[i], time[i+1]-time[i])
output.append(x)
return output
def sample(self, n_samples, steps):
""" Sample from the learned distribution
Parameters
----------
n_samples: int
Number of samples to take
steps: int
Number of steps to make between t=0 and t=1 in the ODE
Returns array (batch_size, steps+1, dim)
Samples of x_t ~ p_t
"""
x_0 = np.random.normal(size=(n_samples, self.dim))
x_1 = self.run(x_0, steps)
return np.array(x_1).swapaxes(0, 1)One we defined our model class, we can instantiate a new flow matching model object.
flow = FlowMatching(n_units=64, n_layers=8)Training
For training we will take a slightly different approach than in the normalizing flow exercise. Here we will make a new dataset object that will inherit from the PyDataset class. This allows us to get random coupling between the base and the data distribution, as well as the random time variable
Whenever we want to get a batch of samples, we will simply take a random subset of rows from the datasaurus dataset. This will be our samples \(x_t\). Samples from the base distribution will be generated by drawing from a bi-variate normal \(x_0 \sim \text{Normal}(0, I)\). Lastly, the time variable will be drawn from a uniform distribution \(t \sim \text{Uniform}(0, 1)\).
Finally, the target velocity is calculated simply as \(v = x_1 - x_0\).
class DataSet(keras.utils.PyDataset):
def __init__(self, batch_size, n_batches, data):
super().__init__()
self.n_batches=n_batches
self.batch_size = batch_size
self.data = data
@property
def num_batches(self):
return self.n_batches
def __getitem__(self, index):
data = self.data
rows = np.random.choice(data.shape[0], size=self.batch_size, replace=True)
data = data[rows]
base = np.random.normal(size=data.shape)
t = np.random.uniform(low=0, high=1, size=data.shape[0])
t = np.repeat(t[:,np.newaxis], repeats=data.shape[1], axis=1)
target = data - base
return dict(x_0=base, x_1=data, t=t), targetWe configure the dataset such that every time we sample from it, we will draw a batch of 512 samples.
epochs=20
batches=1000
batch_size=512
dataset=DataSet(batch_size=batch_size, n_batches=epochs*batches, data=data)Next, we define our learning rate schedule and optimizer. We will use a Cosine Decay and Adam optimizer.
schedule = keras.optimizers.schedules.CosineDecay(initial_learning_rate=0.01, decay_steps=epochs*batches)
optimizer = keras.optimizers.Adam(schedule, global_clipnorm=1.0)Now we can compile the model: we supply the optimizer and add a mean square error loss. This loss will be used to regress the velocity network \(v_\theta\) on the target velocities \(x_1 - x_0\).
flow.compile(
optimizer=optimizer,
loss=keras.losses.MeanSquaredError()
)Because we compiled the model together with an optimizer and a loss, and because we set up our data set object such that it can easily be used on our network, we can simply fit our model with the .fit method - no manual gradient calculation, no manual fitting loop.
history=flow.fit(x=dataset, epochs=epochs, steps_per_epoch=batches)Epoch 1/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 5s 4ms/step - loss: 3.6111
Epoch 2/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 4s 4ms/step - loss: 3.3610
Epoch 3/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 4s 4ms/step - loss: 3.3295
Epoch 4/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 4s 4ms/step - loss: 3.3245
Epoch 5/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.3200
Epoch 6/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 4s 4ms/step - loss: 3.3108
Epoch 7/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2899
Epoch 8/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2719
Epoch 9/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2796
Epoch 10/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2862
Epoch 11/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2628
Epoch 12/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2722
Epoch 13/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2579
Epoch 14/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2366
Epoch 15/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2256
Epoch 16/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2149
Epoch 17/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2062
Epoch 18/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2026
Epoch 19/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.1868
Epoch 20/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step - loss: 3.2060f=plt.plot(history.history["loss"])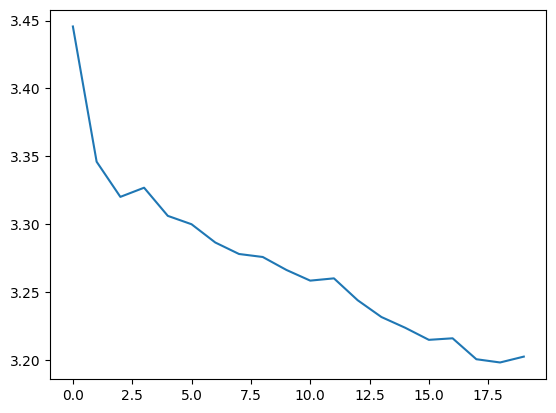
Now that we fitted the model, let’s see the samples it generates!
n_samples=5000
x = flow.sample(n_samples=n_samples, steps=100)
# -1 gets the samples at the last time step, e.i, t=1
f=plt.scatter(x[:, -1, 0], x[:, -1, 1], s=10, alpha=0.5)
f=plt.xlim(-5, 5)
f=plt.xlim(-5, 5)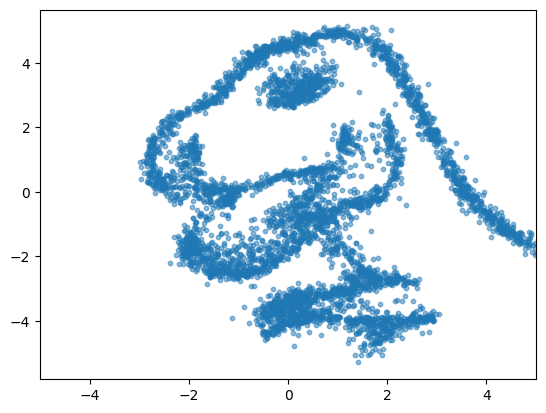
Further exercise
The accuracy of the approximation is generally driven by how expressive the velocity network is, how well it is trained, but also by the accuracy of the integrator. Play around with the network complexity of the flow matching model, simulation budget, and the steps taken during the ODE solver to see how will it affect your ability to generate the datasaurus distribution.